Soal HOTS Jarak Titik, Garis, Dan Bidang Pada Bangun Ruang
-
Suatu aula berbentuk balok dengan perbandingan panjang : lebar adalah 1:1. Sedangkan perbandingan lebar dan tinggi aula adalah 5:2. Di langit-langit aula terdapat lampu yang letaknya tepat pada pusat bidang langit-langit. Pada salah dinding aula dipasang saklar yang letaknya tepat di tengah-tengah dinding. Jika Panjang aula adalah 10 m, jarak saklar ke lampu adalah ….
A. $7$ m
B. $\dfrac72$ m
C. $7\sqrt{29}$ m
D. $\sqrt{29}$ m
E. $\dfrac12\sqrt{29}$ m
Misal aula adalah Balok ABCD.EFGH dengan
$p:l=1:1$ dan $l:t=5:2$ maka $p:l:t=5:5:2$.
diketahui $p = 10$ m sehingga $p=10$ m, $l=10$m, dan $t=4$ m
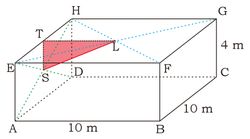
Misalkan lagi lampu adalah L, saklar adalah S dan T adalah titik tengah EH, maka dapat kita gambar seperti berikut
Dari gambar di atas jarak antara saklar dan lampu adalah panjang LS.
Berdasarkan $\vartriangle TLS$ kita dapat mencari panjang LS dengan menggunakan teorema pythagoras.
$$\begin{align*}LS^2&=ST^2+TL^2 \\\ &=(\frac12 CG)^2+(\frac12 AB)^2 \\&=2^2+5^2=29\\ LS&=\sqrt{29} \end{align*}$$ Jadi, jarak antara saklar ke lampu adalah $\sqrt{29}$. (D) 😄 -
Ketika jam pelajaran Dedi tidak mengikuti kegiatan belajar mengajar dikelas. Ia malah duduk-duduk nongkrong di depan kelas ijin keluar alasannya ke kamar mandi. Guru mengetahui perbuatan tersebut dan memberikan teguran bahwa perbuatan tersebut menunjukkan karakter yang kurang baik. Selain ditegur, Dedi juga diberi sanksi untuk menghitung jarak antara titik ke garis diagonal bidang kamar mandi tersebut dan Dedi bisa menghitung dengan tepat. Kamar mandi tersebut berbentuk kubus dan dimisalkan kubus ABCD.EFGH dengan panjang kamar mandi 3 m. Jika dedi menghitung jarak antara titik E ke garis DG, berapakah jawaban Dedi?
A. $3$ m
B. $\frac32 \sqrt{2}$ m
C. $\frac34 \sqrt{2}$ m
D. $\frac32 \sqrt{6}$ m
E. $\frac34 \sqrt{6}$ mDiketahui kubus ABCD.EFGH dengan panjang rusuk 3 m. jarak titik E ke DG?
Perhatikan gambar berikut
Misal N pada DG sehingga jarak E ke DG adalah EN. Kita dapat menentukan panjang EN dengan membuat segitiga bantu $\vartriangle EDG$.
$\vartriangle EDG$ merupakan segitiga sama sisi dengan ED=DG=EG merupakan diagonal bidang kubus. ingat bahwa diagonal bidang kubus dapat kita cari dengan rumus langsung $r\sqrt{2}$ atau dengan teorema pythagoras $$\begin{align*} ED^2&=AB^2+AD^2\\ &=3^2+3^2\\ &=9+9=9\times2\\ ED&=\sqrt{9\times2}\\ ED&=3\sqrt{2} \end{align*}$$ Selanjutnya kita dapat mencari panjang EN pada $\vartriangle EDG$ dengan pythagoras $$\begin{align*} EN^2&=EG^2-NG^2\\&=EG^2-(\frac12 DG)^2\\&=(3\sqrt2)^2-(\frac32\sqrt2)^2\\ &=18-\frac{18}{4}\\&=\frac{72}{4}-\frac{18}{4}=\frac{54}{4}\\ EN&=\sqrt{\frac{54}{4}}\\ EN&=\frac32\sqrt{6} \end{align*}$$ Jadi, jawaban Dedi atas jarak E ke DG adalah $\frac32\sqrt{6}$. (D) 😄 -
Pembelajaran matematika materi dimensi tiga dilakukan dengan diskusi kelompok. Asep sibuk sendiri bermain gadget dan tidak mengikuti diskusi bersama temannya. Setiap kelompok mendiskusikan bagaimana menghitung jarak titik puncak pada bidang empat beraturan ke bidang alas dengan Panjang rusuk 9 m. Ketika presentasi didepan kelas Asep diminta maju mempresentasikan kerja kelompoknya. Asep mempresentasikan bahwa jarak titik puncak pada bidang empat beraturan ke bidang alas adalah merupakan salah satu panjang rusuk bidang empat beraturan. Pernyataan yang tepat tentang hasil presentasi Asep adalah…
A. Jawaban yang dipresentasikan Asep benar yaitu jarak titik puncak ke bidang alas 8 m
B. Jawaban yang dipresentasikan Asep benar yaitu jarak titik puncak ke bidang alas 9 m
C. Jawaban yang dipresentasikan Asep salah, seharusnya jaraknya 3√5 m
D. Jawaban yang dipresentasikan Asep salah, seharusnya jaraknya 3√6 m
E. Jawaban yang dipresentasikan Asep salah, seharusnya jaraknya 9√6 m
Misalkan bidang empat beraturan tersebut adalah ABCD dengan panjang rusuk 9 m dengan puncak titik D dan bidang alas ABC. Titik O merupakan proyeksi titik D terhadap bidang ABC (alas) sehingga jarak puncak ke bidang alasa adalah DO.
Pada bidang empat beraturan semua sisinya berbentuk segitiga sama sisi, untuk itu ingat sifat-sifat segitiga sama sisi
Pada segitiga sama sisi yang panjang rusuknya $a$ berlaku teorema
Luas=$\frac14 a^2\sqrt3$
tinggi=$\frac12 a\sqrt3$Selanjutnya perhatikan gambar bidang empat beraturan berikut
$\vartriangle BCD$ merupakan segitiga sama sisi dengan $BC=BD=CD=9$ m. Titik P ditengah BC sehingga DP merupakan tinggi $\vartriangle BCD$.
Perhatikan segitiga $\vartriangle ADP$. AP merupakan tinggi $\vartriangle ABC$ sehingga AP=DP dan $\vartriangle ADP$ segitiga sama kaki. AP dapat kita cari dengan teorema pada segitiga sama sisi yaitu $$\begin{align*}tinggi&=\frac12 a\sqrt3 \\\ AP=DP&=\frac12\cdot 9\sqrt3 \\ AP=DP&=\frac92\sqrt3 \end{align*}$$ Titik Q pada AD sehingga PQ tegak lurus AD. Kita cari PQ dengan pythagoras $$\begin{align*}PQ^2&=AP^2-AQ^2 \\ &=AP^2-(\frac12 AD)^2 \\ &= (\frac92\sqrt3)^2- (\frac92)^2\\ &= \frac{81}{4}\times3 - \frac{81}{4}=\frac{81}{4}\times2\\ PQ&= \sqrt{\frac{81}{4}\times2}\\ PQ&=\frac92\sqrt2\end{align*}$$ Selanjutnya cari DO menggunakan luas segitiga $\vartriangle ADP$.
$$\begin{align*}L=\cancel{\frac12} AP \times DO&=\cancel{\frac12} AD\times PQ \\\ AP \times DO&= AD\times PQ \\\ DO&=\frac{AD\times PQ}{AP} \\ &=\frac{9\times\cancel{\frac92}\sqrt2}{\cancel{\frac92}\sqrt3}\\ &=\frac{9\sqrt2}{\sqrt3}\times \frac{\sqrt3}{\sqrt3}\\DO&=\frac93\sqrt6=3\sqrt6 \end{align*}$$Jadi, Jawaban yang dipresentasikan Asep salah, seharusnya jaraknya $3\sqrt{6}$ m. (D) 😄
-
Pada kubus ABCD.EFGH dengan Panjang rusuk $8\sqrt{5}$ cm titik P dan Q berturut-turut di tengah garis AB dan GH. Jarak antara garis DP dan garis FQ adalah … A. $20$ cm
B. $20\sqrt{5}$ cm
C. $20\sqrt{10}$ cm
D. $40$ cm
E. $40\sqrt{5}$ cmPerhatikan gambar kubus ABCD.EFGH berikut.
Pada gambar garis DP sejajar dengan FQ sehingga jarak antara DP dan FQ adalah panjang ruas garis PF. Panjang PF dapat kita cari dengan pythagoras pada $\vartriangle PBF$.
$$\begin{align*}PF^2&=PB^2+BF^2\\&=(\frac12 AB)^2+BF^2\\&=(4\sqrt5)^2+(8\sqrt5)^2\\&=80+320=400\\PQ&=\sqrt{400}=20 \end{align*}$$
Jadi, jarak antara garis DP dan garis FQ adalah $20$ cm. (A) 😄
-
Diketahui panjang sebuah rusuk kubus ABCD.EFGH adalah 2022 cm. Titik P, titik Q, titik R, dan titik S berturut-turut merupakan titik tengah dari rusuk AB, BC, EH, dan HG. Hitunglah Jarak bidang FPQ ke bidang DRS.
A. $1011$ cm
B. $1011\sqrt{2}$ cm
C. $2022$ cm
D. $2022\sqrt{2}$ cm
E. $2022\sqrt{3}$ cm
-
Pada balok KLMN.PQRS perbandingan panjang:lebar:tinggi adalah 2:2:3. Jika Panjang balok 8 cm. Tentukan jarak titik K ke titik R.
-
Diketahui kubus ABCD.EFGH mempunyai panjang rusuk 4 kali bulan lahir kamu dengan satuan cm. Titik P pada BC sehingga BP:BC=1:4. Titik Q pada GH sehingga HQ:QG = 1:3, R titik tengah AE. Tentukan jarak R ke PQ.
-
Kubus ABCD.EFGH mempunyai panjang rusuk sama dengan tanggal lahir kamu dalam cm. Titik K pada perpanjangan DA sehingga KA = KD. Tentukan Jarak titik K ke bidang BDHF.
-
Diketahui limas beraturan T.ABCD. panjang rusuk tegak dan panjang rusuk alas 2022 cm. Tentukan jarak titik A ke garis TB.
-
Sebuah limas T.ABCD dimana semua Panjang rusuknya sama yaitu 2 kali nomor absen kamu. Titik P, Q, R, dan S masing-masing terletak ditengah-tengah AB, CD, TD, dan TA. Tentukan jarak PQRS dan TBC.
Dari gambar di atas jarak antara saklar dan lampu adalah panjang LS.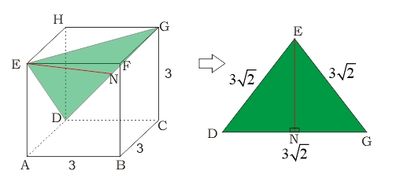 
Misal N pada DG sehingga jarak E ke DG adalah EN. Kita dapat menentukan panjang EN dengan membuat segitiga bantu $\vartriangle EDG$. 
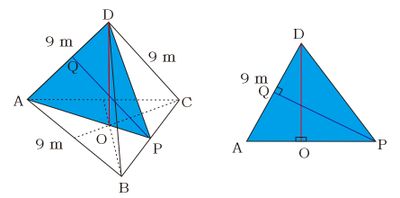$\vartriangle BCD$ merupakan segitiga sama sisi dengan $BC=BD=CD=9$ m. Titik P ditengah BC sehingga DP merupakan tinggi $\vartriangle BCD$. 
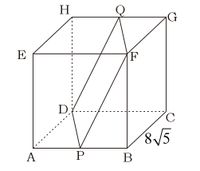Pada gambar garis DP sejajar dengan FQ sehingga jarak antara DP dan FQ adalah panjang ruas garis PF. Panjang PF dapat kita cari dengan pythagoras pada $\vartriangle PBF$.
$$\begin{align*}PF^2&=PB^2+BF^2\\&=(\frac12 AB)^2+BF^2\\&=(4\sqrt5)^2+(8\sqrt5)^2\\&=80+320=400\\PQ&=\sqrt{400}=20 \end{align*}$$
Jadi, jarak antara garis DP dan garis FQ adalah $20$ cm. (A) 😄