Aljabar Vektor Pada Bangun Datar (Ruang Dimensi 2)

Bakhtiar Rifai Bakhtiar Rifai
Aljabar Vektor pada Bangun Datar (Ruang Dimensi 2)

Vektor dimensi dua adalah vektor yang mempunyai dua unsur yaitu unsur vertikal (sumbu Y) dan horizontal (sumbu X). Vektor pada bidang datar (dimensi dua) ditandai dengan sumbu X dan sumbu Y, yang saling berpotongan di titik pusat O (0, 0). Secara analitis vektor dimensi dua dapat disajikan menurut unsur-unsurnya yaitu:

Dengan x adalah unsur mendatar. Apabila $x > 0$ (positif) maka x mempunyai arah ke kanan dan apabila $x < 0$ (negatif) x mempunyai arah ke kiri. Selanjutnya y adalah unsur vertikal. Apabila $y > 0$ (positif) maka arahnya ke atas dan jika $y < 0$ (negatif) arahnya ke bawah.

1. Komponen Vektor, Vektor Kolom, dan Vektor Baris

Perhatikan vektor pada gambar berikut 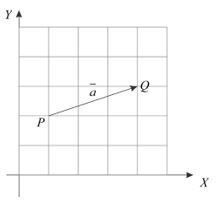Vektor Kolom Secara umum vektor $\vec{a}$ pada gambar diatas dapat ditulis secara kolom sebagai berikut $$\vec{PQ}=\vec{a}=\begin{pmatrix} 3 \\ 1 \end{pmatrix}$$ selain dengan vektor kolom, vektor $\vec{a}$ juga dapat ditulis dengan vektor baris seperti berikut $$\vec{PQ}=\vec{a}=\begin{pmatrix} 3, 1\end{pmatrix}$$

$\begin{pmatrix} 3 \\ 1 \end{pmatrix}$ disebut Vektor kolom dan $\begin{pmatrix} 3, 1\end{pmatrix}$ disebut vektor baris. 3 dan 1 merupakan komponen dari Vektor $\vec{a}$.

Vektor yang digambarkan pada bidang koordinat mempunyai komponen horisontal (gerakan ke kanan/kiri) dan komponen vertikal (gerakan ke atas/bawah). Oleh karena itu, vektor dapat disajikan secara kolom. Komponen Vektor $$\vec{PQ}=\begin{pmatrix} \text{Komponen horisontal} \\ \text{komponen vertikal}\end{pmatrix}$$

2. Vektor Posisi

Vektor Posisi adalah vektor yang berpangkal di pusat koordinat $O(0,0)$ dan berujung di suatu titik $(x,y)$. Perhatikan sebarang titik $A(x_1, y_1)$ dan titik $B(x_2, y_2)$ pada koordinat Cartesius berikut. 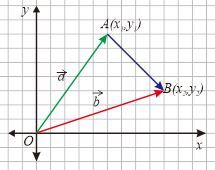Vektor Posisi Pada gambar di atas, vektor $\vec{a}$ mewakili ruas garis berarah dari titik pangkal $O(0, 0)$ ke titik $A(x_1, y_1)$ atau vektor $\vec{OA}$. Oleh karena itu, vektor $\vec{a}$ dapat dituliskan dalam bentuk vektor kolom
$\vec{OA}=\vec{a} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix}$
Adapun vektor $\vec{b}$ mewakili ruas garis berarah dari titik pangkal $O(0, 0)$ ke titik $B(x_2, y_2)$ atau vektor $\vec{OB}$. Vektor $\vec{b}$ dapat dituliskan sebagai
$\vec{OB}=\vec{b} = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix}$

Sekarang perhatikan vektor $\vec{AB}$. Vektor $\vec{AB}$ kita dapatkan dengan cara menarik garis dari titik A ke titik B. Seperti yang sudah dipelajari sebelumnya, vektor $\vec{AB}$ dapat dinyatakan dalam bentuk penjumlahan vektor secara geometri yaitu $\vec{AB}=\vec{OB}-\vec{OA}$ sehingga $$\begin{align*} \vec{AB}&=\vec{OB}-\vec{OA} \\ &=\vec{b}-\vec{a}\\ &= \begin{pmatrix}x_2\\y_2\end{pmatrix}-\begin{pmatrix}x_1\\y_1\end{pmatrix}\\ \vec{AB} &=\begin{pmatrix}x_2-x_1\\y_2-y_1\end{pmatrix} \end{align*}$$

3. Modulus atau Besar Vektor

Modulus menyatakan panjang atau besar vektor. Karena panjang atau besar vektor selalu bernilai positif maka cara menulis modulus menggunakan tanda mutlak $\left( \lvert {} \rvert \right)$. 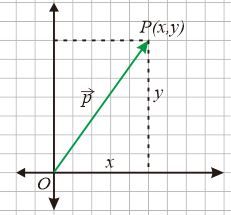Panjang Vektor Jika diketahui koordinat titik $P (x, y)$ maka panjang vektor posisi $\vec{OP}=\begin{pmatrix} x \\ y \end{pmatrix}$ dirumuskan dengan dalil pythagoras atau sebagai berikut $\lvert \vec{OP} \rvert=\sqrt{x^2+y^2}$.

Contoh 1
Diketahui Vektor $\vec{OQ}=\vec{q}=\begin{pmatrix}3 \\4 \end{pmatrix}$. Tentukan Panjang Vektor $\vec{q}$

Alternatif penyelesaian
$$\begin{align*} & \lvert \vec{q} \rvert=\sqrt{3^2+4^2}\\ & \lvert \vec{q} \rvert=\sqrt{25}\\& \lvert \vec{q} \rvert=5\end{align*}$$ Jadi, Panjang Vektor $\vec{q}$ adalah 5 satuan

4. Vektor satuan

Pada pembahasan sebelumnya, vektor satuan dari vektor $\vec{a}$ dirumuskan: $e_{\vec{a}}=\frac{\vec {a}}{\lvert \vec{a} \rvert}$ atau $\widehat{a}=\frac{\vec{a}}{\lvert \vec{a} \rvert}$

Dalam Vektor kolom, jika $\vec{a}=\begin{pmatrix} x \\ y \end{pmatrix},$ maka $\widehat{a}=\frac{1}{\sqrt{x^2+y^2}}.\begin{pmatrix} x \\ y \end{pmatrix}$

5. Sifat Operasi Vektor kolom

a. Penjumlahan Vektor

Secara analisis, Penjumlahan dua vektor dapat dikerjakan sebagai berikut
$$\vec{a}+\vec{b} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix}+\begin{pmatrix} x_2 \\ y_2 \end{pmatrix}=\begin{pmatrix} x_1+x_2 \\ y_1+y_2 \end{pmatrix}$$ Apabila kedua vektor diketahui mengapit sudut tertentu, maka dapat digunakan perhitungan dengan memakai rumus aturan cosinus seperti pada trigonometri. 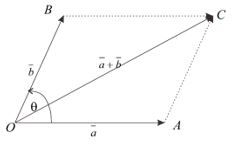Penjumlahan Vektor Apabila sudut antara $\vec{a}$ dan $\vec{b}$ adalah $\theta$, maka $$\begin{align*} {\lvert \vec{a}+\vec{b} \rvert}^2&=\lvert \vec{a} \rvert+\lvert \vec{b} \rvert+2\lvert \vec{a} \rvert\lvert \vec{b} \rvert \cos \theta \\ \lvert \vec{a}+\vec{b} \rvert&=\sqrt{\lvert \vec{a} \rvert+\lvert \vec{b} \rvert+2\lvert \vec{a} \rvert\lvert \vec{b} \rvert\cos \theta } \end{align*}$$

Jika vektor disajikan dalam bentuk komponen (dalam bidang kartesius) maka penjumlahan dapat dilakukan dengan menjumlahkan komponennya.

Misalnya:
$\vec{a} = \begin{pmatrix} x_A \\ y_A \end{pmatrix}$ dan $\vec{b}$ = $\begin{pmatrix} x_B \\ y_B \end{pmatrix}$ maka $\vec{a}+\vec{b} = \begin{pmatrix} x_A+x_B \\ y_A+y_B \end{pmatrix}$

Contoh 2
Diketahui vektor $\vec{a}=\begin{pmatrix} 2 \\ -3 \end{pmatrix}$ dan vektor $\vec{b}=\begin{pmatrix} -4 \\ 3 \end{pmatrix}$. Tentukan penjumlahan vektor dari $\vec{a}+\vec{b}$!
Alternatif Penyelesaian
$\vec{a}+\vec{b}$ = $\begin{pmatrix} 2+(-4) \\ -3+3 \end{pmatrix}=\begin{pmatrix} -2 \\ 0 \end{pmatrix}$

Contoh 3
Diketahui panjang vektor |$\vec{a}$| = 2 dan panjang vektor |$\vec{b}$| = 4, sudut antara vektor $\vec{a}$ dan $\vec{b}$ adalah $60^\circ$, maka :

$$\begin{align*}\lvert \vec{a}+\vec{b} \rvert&=\sqrt{\lvert \vec{a} \rvert+\lvert \vec{b} \rvert+2\lvert \vec{a} \rvert \lvert \vec{b} \rvert \cos \theta } \\ &= \sqrt{2^2+4^2+2.2.4.\cos 60^\circ} \\ &= \sqrt{4+16+16.\tfrac{1}2} \\ &= \sqrt{28}\\ &=2\sqrt{7} \end{align*}$$

b. Pengurangan Vektor

Secara analitis, jika diketahui Vektor $\vec{a}=\begin{pmatrix} a_1 \\ a_2 \end{pmatrix}$ dan $\vec{b}=\begin{pmatrix} b_1 \\ b_2 \end{pmatrix}$ maka pengurangan dua Vektor dapat dirumuskan $\vec{a}-\vec{b}=\begin{pmatrix} a_1-b_1 \\ a_2-b_2 \end{pmatrix}$ 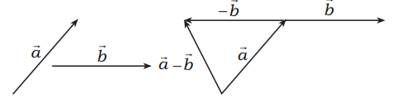Pengurangan Vektor Contoh 4 Diketahui vektor $\vec{p}=\begin{pmatrix} 6 \\ -3 \end{pmatrix}$ dan vektor $\vec{q}=\begin{pmatrix} -4 \\ 3 \end{pmatrix}$. Tentukan vektor dari $\vec{p}-\vec{q}$!
Alternatif Penyelesaian
$\vec{p}-\vec{q}$ = $\begin{pmatrix} 6-(-4) \\ -3-3 \end{pmatrix}=\begin{pmatrix} 10 \\ -6 \end{pmatrix}$

c. Perkalian Skalar dengan Vektor

Perkalian skalar dengan vektor akan menghasilkan vektor dengan arah yang sama. Vektor $\vec{v}$ sejajar dengan vektor $\vec{u}$, ditulis $\vec{v}//\vec{u}$ jika:

  • Jika $k > 0$, maka $\vec{v}$ searah $\vec{u}$
  • Jika $k < 0$, maka $\vec{v}$ berlawanan $\vec{u}$ Perkalian Vektor

Secara analitis, jika diketahui Vektor $\vec{a}=\begin{pmatrix} a_1 \\ a_2 \end{pmatrix}$maka $k.\vec{a}=\begin{pmatrix} k.a_1 \\ k.a_2 \end{pmatrix}$, dengan $k$ sebuah konstanta. Contoh 5
Diketahui $\vec{a} = \begin{pmatrix} -2 \\3 \\\end{pmatrix}$ dan $\vec{b} = \begin{pmatrix}4 \\-2 \\\end{pmatrix}$ tentukanlah $3\vec{b} – \frac{1}{2}\vec{a}$! Alternatif Penyelesaian
$$\begin{align*} 3\vec{b} – \frac{1}{2}\vec{a}&=3 \begin{pmatrix} -2 \\3 \\\end{pmatrix}-\frac{1}{2}\begin{pmatrix}4 \\-2 \\\end{pmatrix}\\ &= \begin{pmatrix} 3.(-2) \\3(3) \\\end{pmatrix}-\begin{pmatrix}\frac{1}{2}(4) \\\frac{1}{2}(-2) \\\end{pmatrix}\\&= \begin{pmatrix} -6 \\9 \\\end{pmatrix}-\begin{pmatrix}2 \\ -1 \\\end{pmatrix}\\&=\begin{pmatrix}-6-2 \\ 9-(-1) \\\end{pmatrix}\\&=\begin{pmatrix}-8 \\ 10 \\\end{pmatrix} \end{align*}$$ Contoh 6
Tentukan apakah titik-titik P(1, –2), Q(2, 1), dan R(4, 7) kolinear (segaris).
Alternatif Penyelesaian:
Titik P, Q dan R dikatakan kolinear (segaris) jika titik P, Q dan R terletak pada garis yang sama. Titik P, Q dan R akan terletak pada garis yang sama jika dan hanya jika vektor-vektor yang mewakili ruas garis berarah dari titik-titik P, Q dan R memiliki pangkal yang sama dan sejajar.
Vektor $\vec{PQ}$ dan $\vec{PR}$ memiliki titik pangkal yang sama.
Komponen vektor $\vec{PQ}=\vec{q}-\vec{p}=\begin{pmatrix}2 \\ 1 \end{pmatrix}-\begin{pmatrix}1 \\ -2 \end{pmatrix}=\begin{pmatrix}1 \\ 3 \end{pmatrix}$
Komponen vektor $\vec{PR}=\vec{r}-\vec{p}=\begin{pmatrix}4 \\ 7 \end{pmatrix}-\begin{pmatrix}1 \\ -2 \end{pmatrix}=\begin{pmatrix}3 \\ 9 \end{pmatrix}$

Dua vektor segaris jika ada bilangan $k$ yang memenuhi $\vec{PR}=k.\vec{PQ}$ dan kedua vektor berpangkal yang sama. $$\begin{align*} \vec{PR}&=\begin{pmatrix}3 \\ 9 \end{pmatrix}\\ &= 3\begin{pmatrix}1 \\ 3 \end{pmatrix}\\\vec{PR}&= 3\vec{PQ} \end{align*}$$ Karena $\vec{PR}=3\vec{PQ}$ berarti vektor $\vec{PQ}$ sejajar vektor $\vec{PR}$ dan sama-sama berpangkal di titik P. Jadi, dapat disimpulkan bahwa titik P, Q dan R merupakan titik-titik yang kolinear (segaris).

d. Kesamaan dua Vektor

Secara analitis, dua Vektor $\vec{a}=\begin{pmatrix} a_1 \\ a_2 \\ \end{pmatrix}$ dan $\vec{b}=\begin{pmatrix} b_1 \\ b_2 \\ \end{pmatrix}$ dikatakan sama jika dan hanya jika $a_1=b_1$ dan $a_2=b_2$

4. Basis Normal Standar

Definisi basis

Jika masing-masing vektor tersebut panjangnya 1 satuan dan saling tegak lurus , maka $\vec{v}_1,\vec{v}_2,\vec{v}_3,…,\vec{v}_n$ itu disebut basis normal standar dalam ruang $V$

Berdasarkan definisi tersebut maka kita dapat menyimpulkan bahwa vektor-vektor:

  1. $\widehat{i}=\begin{pmatrix} 1 \\0 \\\end{pmatrix}$ dan $\widehat{j}=\begin{pmatrix}0 \\1 \\\end{pmatrix}$ adalah basis normal standar dalam ruang vektor $R^2$ dengan $\widehat{i}$ dan $\widehat{j}$ masing-masing sejajar dengan sumbu X dan Y

  2. $\widehat{i}=\begin{pmatrix}1 \\0 \\0 \\\end{pmatrix},$ $\widehat{j}=\begin{pmatrix}0 \\1 \\0 \\\end{pmatrix}$ dan $\widehat{k}=\begin{pmatrix}0 \\0 \\1 \\\end{pmatrix}$adalah basis normal standar dalam ruang vektor $R^3$ dengan $\widehat{i}$, $\widehat{j}$ dan $\widehat{k}$ sejajar dengan sumbu X, Y, dan Z.

Dengan demikian, jika P sebuah titik (x,y) dan O(0,0), maka Vektor posisi $\vec{OP}$ dapat ditulis sebagai kombinasi dari dua Vektor basis $\vec{OP}=\vec{p}=\begin{pmatrix}x \\ y \\ \end{pmatrix}=x\begin{pmatrix} 1\\ 0\\ \end{pmatrix}+y\begin{pmatrix} 0\\ 1\\ \end{pmatrix}=x\widehat{i}+y\widehat{j}$

Contoh 7
Diketahui segitiga OAB dengan titik sudut: O(0, 0), A(3, 1) dan B(6, 5). $\vec{a}$ merupakan vektor posisi dari titik 𝐴 dan $\vec{b}$ vektor posisi dari titik 𝐵. Nyatakan vektor $\vec{a}$, $\vec{b}$ dan $\vec{AB}$ dalam bentuk vektor basis.
Alternatif penyelesaian:
$\vec{a}=x_1\widehat{i}+y_1\widehat{j}=3\widehat{i}+\widehat{j}$
$\vec{b}=x_1\widehat{i}+y_1\widehat{j}=6\widehat{i}+5\widehat{j}$
$\vec{AB}=\vec{b}-\vec{a}=(6\widehat{i}+5\widehat{j})-(3\widehat{i}+\widehat{j})=3\widehat{i}+4\widehat{j}$

Latihan 3

  1. Perhatikan gambar vektor di samping :
    Gambarlah vektor Gambarlah vektor :
    1. $3.\vec{u}$
    2. $-2.\vec{v}$
    3. $\vec{u} + \vec{v}$
    4. $2.\vec{u} – \vec{v}$
  2. Jika diketahui $\vec{u} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}$ dan $\vec{v} = \begin{pmatrix}-4 \\ 1 \end{pmatrix}$ tentukanlah :
    1. $\vec{u}$
    2. $-3.\vec{v}$
    3. $3.\vec{u} + 2.\vec{v}$
    4. $2.\vec{v} – \vec{u}$
  3. Diketahui vektor $\vec{a} = \begin{pmatrix}2 \\-1 \\\end{pmatrix}$ dan $\vec{b} = 2.\vec{a}$ , tentukanlah vektor $\vec{c} = \vec{a} + \vec{b}$
  4. Diketahui vektor $\vec{a} = \begin{pmatrix}-2 \\ 4 \\ \end{pmatrix}$, $\vec{b} = \begin{pmatrix} x \\ y \\ \end{pmatrix}$ dan c = $\begin{pmatrix}3 \\5 \\\end{pmatrix}$. Tentukan x dan y jika $\vec{c} = \vec{a} + \vec{b}$
  5. Jika vektor $\vec{m} = \begin{pmatrix}-8 \\4 \\\end{pmatrix}$ dan $\vec{n} = \begin{pmatrix}10 \\-6 \\\end{pmatrix}$ tentukanlah secara aljabar vektor dari :
    1. $\frac{1}{2} \vec{m} – \frac{1}{2} \vec{n}$
    2. $\frac{1}{4} \vec{m} + \frac{1}{2} \vec{n}$
  6. Diketahui $\vec{a} = \begin{pmatrix} -4 \\-2 \\\end{pmatrix}$ dan $\vec{b} = \begin{pmatrix}1 \\4 \\\end{pmatrix}$ tentukanlah $3\vec{b} – \frac{1}{2}\vec{a}$!
  7. Jika $\vec{a} = \begin{pmatrix}2 \\5 \\\end{pmatrix}$ dan $\vec{b} = \begin{pmatrix}3 \\-7 \\ \end{pmatrix}$ tentukanlah $2\vec{a} – \frac{1}{2}\vec{b}$!
  8. Jika $\vec{p} = \begin{pmatrix}5 \\-3 \\\end{pmatrix}$ dan $\vec{q} = \begin{pmatrix}4 \\-2 \\\end{pmatrix}$ tentukanlah $\frac{1}{2}\vec{b} – \frac{1}{2}\vec{q}$!
  9. Jika diketahui $\vec{p} = \begin{pmatrix}4 \\-6 \\\end{pmatrix}$ dan $\vec{q} = \begin{pmatrix}x \\y \\ \end{pmatrix}$ tentukanlah x dan y jika $\vec{p} + \vec{q} = \begin{pmatrix}-2 \\-3 \\ \end{pmatrix}$!
  10. Jika $\vec{a} = \begin{pmatrix}a_1 \\a_2 \\\end{pmatrix}$ dan $\vec{b} = \begin{pmatrix}-9 \\2 \\\end{pmatrix}$ tentukanlah $a_1$ dan $a_2$ jika $\vec{a} – \vec{b} = \begin{pmatrix}4 \\7 \\\end{pmatrix}$!
Menulis Dengan Bicara Atau Suara Di HP
Persamaan Lingkaran Memenuhi Kriteria Tertentu

Artikel Terkait

Komentar